
How do scale ceilings affect “compensation demand” survey responses?
How do scale ceilings affect “compensation demand” survey responses? This methodology experiment - part of our ongoing Methodology matters series - explorers numeric slider questions.
Summary and takeaway
The results of this experiment provide evidence that when writing survey questions that involve numeric sliders, the selection of a ceiling value (i.e., the maximum response permitted) affects responses in important ways. Ceilings change not only the distribution of responses, but also the share of responses at the ceiling.
Using a sliding scale, survey respondents were asked to report the price they would need to be paid to complete an activity involving discussion of their political opinions. The ceiling on the scale was randomly assigned between $50, $100, and $200. We found that increasing the ceiling price in this manner monotonically increased the mean price reported while decreasing the proportion of respondents hitting the ceiling. We discuss the implications of these findings for survey research in subsequent sections.
Introduction and background
When asking questions with numeric responses, survey researchers face a dilemma: either allow for open-ended responses which potentially invite outliers, or provide a sliding scale with a floor and a ceiling (i.e., a scale minimum and a scale maximum). This tradeoff is particularly salient for social science researchers relying on “willingness to pay” or “compensation demand” measures to study respondents’ preferences. In this article, we focus specifically on compensation demand measures (see this article for an example), which invite respondents to report the price they would like to be paid for completing an activity, namely one that respondents may disenjoy.
Though floors and ceilings preclude outliers, their disadvantages are threefold. First, if the ceiling is lower than the prices respondents would provide as open-ended responses, it may serve to artificially restrict the range of responses. Setting a $200 ceiling when an unconstrained answer would be $500 serves to bias responses compared to an open-ended question; we refer to this as the “cutoff” mechanism. Second, a ceiling can serve as an anchor, shifting responses across the range of the distribution; we refer to this as an “anchor” effect. Consider a respondent who consistently responds at 50% of the listed ceiling and whose response is not cut off by the ceiling but is changed by it. This type of anchoring has been subject to much inquiry in the psychology and economics literature on measurement and survey design; notably, this literature acknowledges that anchoring sometimes is externally valid because real-world scenarios may involve anchors. Third, price ceilings could interact with other treatments by affecting the degree to which they are subject to ceiling effects, such that observed treatment effects are sensitive to price ceilings.
We explore these mechanisms in this brief writeup. Ultimately, we find clear evidence that price ceilings work through both restricting and shifting responses—i.e., via the aforementioned “cutoff” and “anchor” mechanisms. However, we find little evidence of interactions between randomized price ceilings and other treatments, in part because we tested a pilot treatment that proved to be ineffective.
Experimental setup
To evaluate the effect of price ceilings on responses, we fielded a survey experiment. All respondents were asked how much they would need to be paid to complete a hypothetical activity by making a video expressing their political beliefs on a controversial topic. The question was formatted as a slider with a $0 floor and scale points measured with 2 decimal places (to represent cents).
Respondents were randomized per a 3-by-2 factorial design. First, respondents were randomized between a $50 ceiling, a $100 ceiling, or a $200 ceiling. Respondents were then assigned to a treatment that provided information about how co-partisan Americans respond to political differences or a control condition; we refer to this as the tolerance treatment. Respondents were then asked to answer the price question one more time. Those who saw a $50 ($100/$200) ceiling for the pre-treatment price question also saw a $50 ($100/$200) ceiling for the post-treatment price question. In short, two prices were observed for all respondents, and the randomly assigned ceiling was constant for pre- and post-treatment prices within-respondent.
Methods and Data
We pre-registered six hypotheses which we assess using covariate-adjusted linear regression with a pre-registered set of covariates. In the Results section, we describe each hypothesis and the corresponding results in turn, leaving aside Hypothesis 5 which featured a different outcome not involving numeric scales or compensation demands. Our final analysis involves 2,300 responses (with some respondents excluded from a total sample of 3000 due to pre-treatment piping errors).
Results
We first show the spread of the data across pre-treatment price responses. The faceted histogram below offers visual confirmation that increasing the price ceiling from $50 to $100 and then $200 monotonically increases the mean price reported and monotonically decreases the share of respondents reporting the ceiling price. These patterns are examined formally with a series of hypothesis tests, reported below.
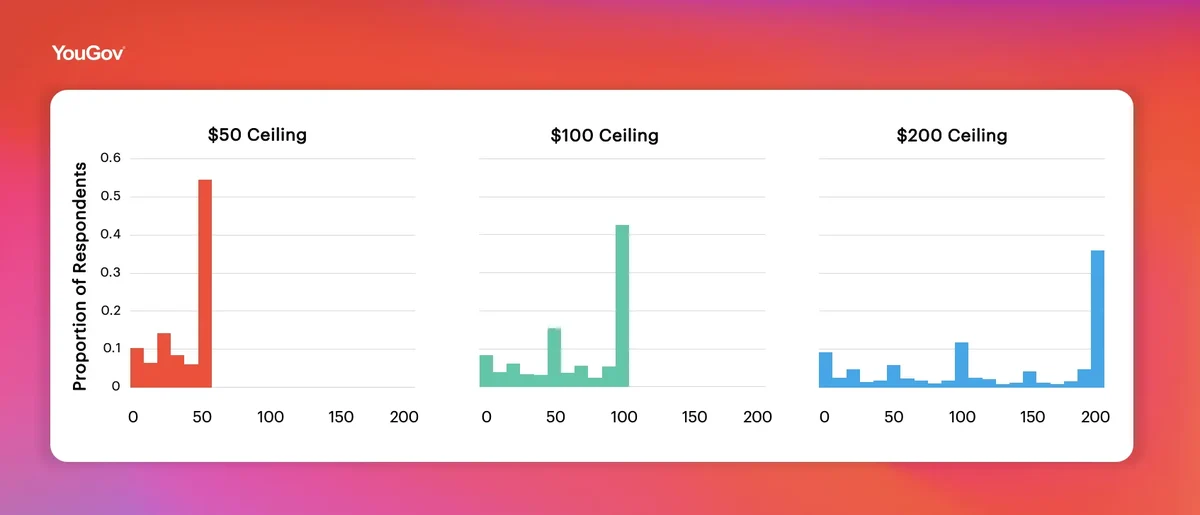
Hypothesis 1: Increasing the price ceiling (from $50 to $100, then $200) increases the average price reported by respondents.
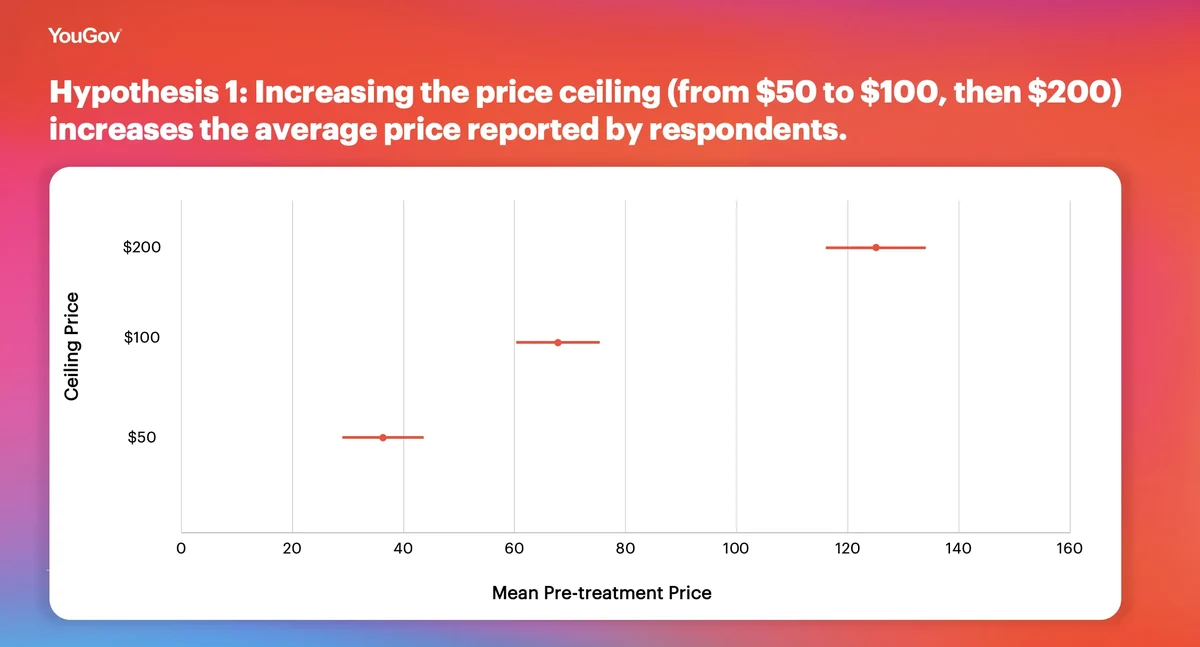
The figure above, which shows the estimated marginal mean of each ceiling condition, offers support for Hypothesis 1. Ceiling values exhibit “anchor effects” by altering the mean price reported. This hypothesis is assessed only using pre-treatment price measures so the only relevant randomization is the price ceiling. We note that while the average price increases for higher ceilings, the relationship between price and ceilings is non-linear, the mean price goes from 72.6% of the ceiling at $50 to 62.5% of the ceiling at $200.
While anchoring may not directly implicate the estimation of average treatment effects in an experimental context, these results suggest researchers should use caution when interpreting the substantive meaning of compensation demand responses.
Hypothesis 2: Increasing the price ceiling decreases the percentage of respondents answering the maximum price.
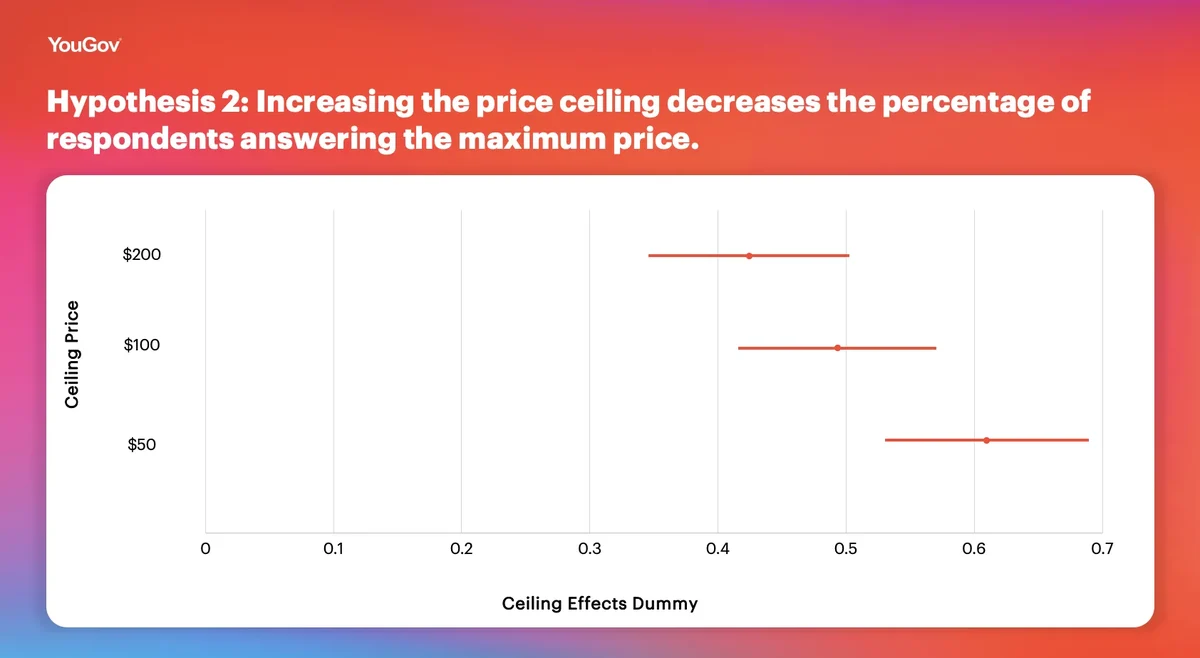
The figure above, which describes the share of respondents at the ceiling for pre-treatment prices, provides support for Hypothesis 2. This share is noticeably higher for the higher ceiling prices. Moreover, these results imply that an amalgam of cutoff and anchoring effects is likely at play. If the ceiling operated only by cutting off prices that were too high and not by changing the broader distribution of prices, the gap in share of responses at the price ceiling would be far higher. In addition, the mean pretreatment price in the $50 condition (approximately $36.30) would be far closer to $50.
Because ceilings serve through an anchoring mechanism to expand or constrict the range of responses, they may implicate the estimation of treatment effects. Consider in this case an individual unaffected by cutoff effects but affected by anchoring effects that constrict responses such that a $20 treatment effect becomes $10. This is in addition to the more obvious interaction between cutoffs and treatment effects: Consider an individual whose response would be at the $50 ceiling in the control condition and who would exhibit an individual treatment effect of 0 even if the treatment increased compensation demand (because the higher demand would be constricted at the same ceiling). At a $100 ceiling, however, the same individual could have an initial response at $75 and a post-treatment response of $85.
Hypothesis 3: Increasing the price ceiling increases respondents’ pre-/post-treatment difference in price (by diminishing ceiling effects).
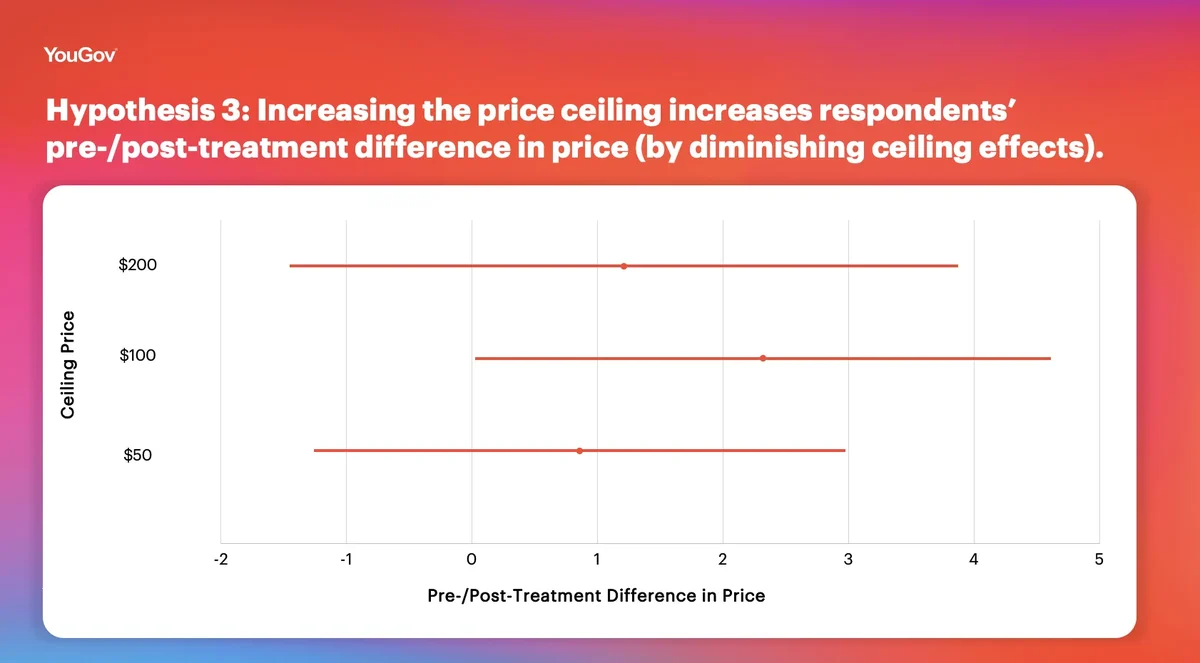
As we can see in the figure above, hypothesis 3 does not appear to be supported. There is no statistically significant or substantive difference between the pre/post price differences across ceiling levels. A reasonable explanation is that there is little difference between pre- and post-treatment prices pooling across all conditions. If ceilings serve to artificially restrict or expand treatment effects, they do so in comparison to a small baseline movement.
Hypothesis 4: The tolerance condition will lower the post-treatment prices compared to the control condition (pooling across the ceiling conditions).
Hypothesis 6: Increasing the price ceiling increases the average treatment effect of the “tolerance” treatment.
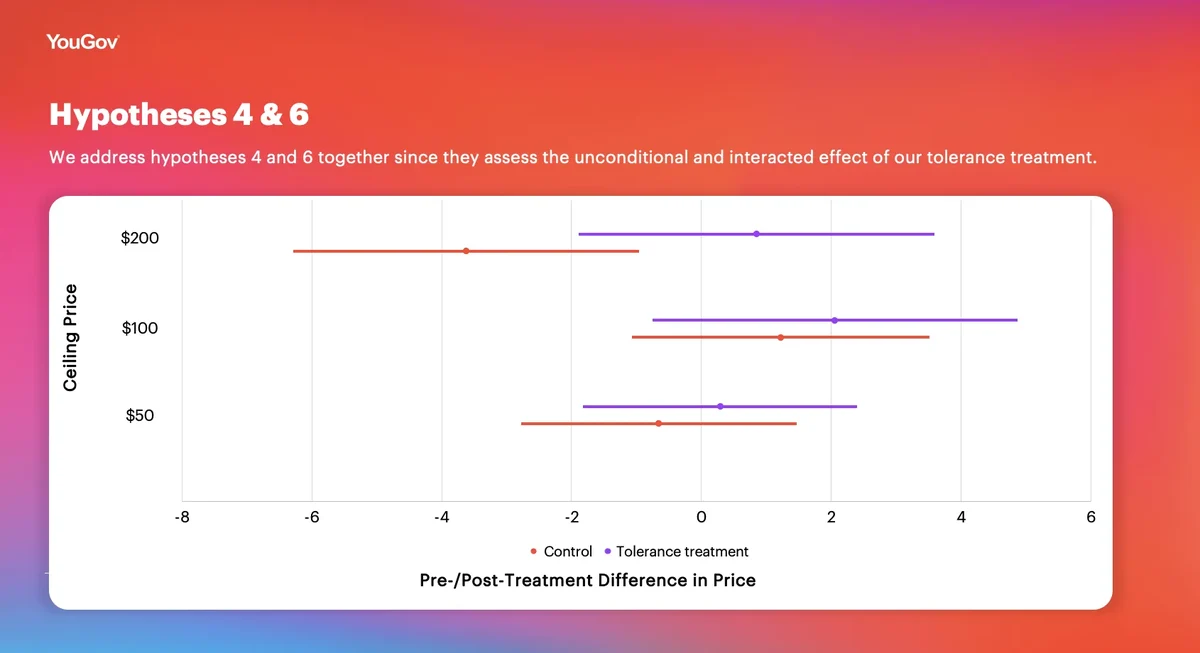
We address hypotheses 4 and 6 together since they assess the unconditional and interacted effect of our tolerance treatment. This treatment, pooled across ceiling levels, had neither a substantively nor a statistically significant effect on prices. As such, none of these 3 hypotheses are supported. However, we believe this says little about the causal relationship between ceiling effects and effective treatments. The graph below shows that our estimand for the tolerance treatment, the difference in pre-and post-treatment prices for treated compared to control individuals, is small and cannot be differentiated from zero across all three price ceiling conditions.
Conclusion and General discussion
The results of this experiment clearly show that price ceilings both shift the share of respondents at the ceiling and change the distribution of responses over the distribution. However, in part due to the nature of the tested treatment, we have less conclusive evidence about the interaction between price ceilings.
Future work in this area could proceed down two paths. First, the interaction between price ceiling and treatment may be affected by the type, expected direction, and efficacy of the treatment. Our piloted treatment had relatively little effect on our price outcomes. As such, our hypotheses about the relationship between treatment effects and ceilings could not be clearly addressed. Further investigations could explore how price ceilings affect a range of treatments.
Second, a broader potential outcomes framework can more comprehensively assess the role of ceiling effects by exploring how individual treatment effects in hypothetical full schedules of potential outcomes are affected. These mechanisms might differ across the types of beliefs that are operationalized through price measures; in other words, whether cutoff effects or anchor effects are more pertinent for a given experiment may hinge upon the latent quantity being studied. For example, a strongly held attitude could be subject to no anchor effects but only cutoff effects, as in survey outcomes that measure recall of known facts. In contrast, a weakly held belief with a distribution that falls below an plausible ceiling could be subject to anchor effects but no cutoff effects across a range of possible ceilings. An outcome with these characteristics might result in respondents who answer a constant or near constant share of a ceiling.
In a context where real money is on the line, we expect that cutoff effects will dominate anchor effects. This is because price demands might be less responsive to a variety of contextual effects, including anchoring. Instead, the primary effect of a price ceiling would be to artificially cut off some response that would be above the ceiling. Future work should explore these dynamics across more diverse substantive settings.
About this study
See the survey disclosure document here.
About the authors
Daniel Markovits is a PhD candidate in political science at Columbia University. His research focuses on how Americans respond to perceptions that democracy is threatened. He uses survey and field experiments. More information about his work can be found here.
Patrick Liu is a PhD student in political science at Columbia University. His research examines how deeply held political beliefs and attitudes respond to interpersonal conversations, tailored persuasive messages, and social influence.
About Methodology matters
Methodology matters is a series of research experiments focused on survey experience and survey measurement. The series aims to contribute to the academic and professional understanding of the online survey experience and promote best practices among researchers. Academic researchers are invited to submit their own research design and hypotheses.